Science Advance.
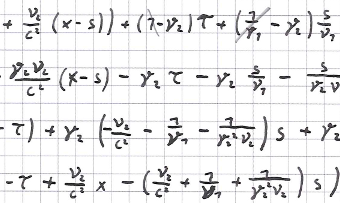
Physik:
Nachgerechnet
Die Uhren laufen schneller, weil die Relativgeschwindigkeit, mit der man sich in einem Schwerefeld und im Sonnensystem mitbewegt, je nach Höhe unterschiedlich ist.
Je größer die Geschwindigkeit desto größer die Trägheit. Die Masse bleibt immer gleich, nur die Trägheit (Lorentzfaktor gamma) nimmt zu. Damit verändert der Faktor gamma weder die absolute Masse noch die absolute Geschwindigkeit. Dass dies stimmt, wird durch die Rotationswellenenergie von Protonen erhärtet, die nicht von ihrer Geschwindigkeit im Beschleuniger abhängt. Physiker gehen heutzutage ebenso von einer nicht veränderlichen, absoluten Masse aus und schreiben den Lorentzfaktor einem veränderlichen Impuls zu.
Auch wird die Zeit nicht durch Massen an sich, sondern durch die Gravitationskraft dilatiert. Im Weltraum, wo annähernd Schwerelosigkeit herrscht, läuft die Zeit 1,0000000007 mal schneller. Dies liegt an der Geschwindigkeit, mit der man sich im Gravitationsfeld eines Planeten dreht. Durch den Faktor gamma entsteht hier eine Trägheitszunahme von genau 1,0000000007, weswegen die Zeit im Weltall schneller vergeht. Auf einem 3000 m hohen Berg vergeht die Zeit um 30 Nanosekunden schneller. Dies ist ca. 43 mal schneller als im All. Auf einem schweren Berg ist g um 1,00089 mal größer, obwohl man da etwas weiter vom Erdmittelpunkt entfernt ist, einfach durch die nahe Gravitation des massiven Berges selbst, womit die Relativgeschwindigkeit um 1,000000021 ggü. der Schwerelosigkeit zunimmt. Auch weniger als ein Meter höher zeigen Atomuhren unterschiedliche Zeiten an. Wenn man für r 6731000+1 m annimmt und dies in den Lorentzfaktor einfügt, würden Uhren 1 m höher aufgrund dessen um 0,3 ns schneller laufen.
"Die Uhren laufen schneller, weil die Relativgeschwindigkeit, mit der man sich in einem Schwerefeld und im Sonnensystem mitbewegt, je nach Höhe unterschiedlich ist"
Fazit: es gibt eine Zeitdilatation, die aber aufgrund der Massenträgheit bei größerer Geschwindigkeit nahe dem Mittelpunkt eines Schwerefelds zustandekommt, weil t=v/a=√(mG/r)/a ist, weiter oben nimmt v aufgrund von r ab und das Verhältnis des Lorentzfaktor im Nanobereich zu. Damit ist der Impuls nicht mit der Zeit t' verknüpft, die bei veränderlichem Impuls konstant sein muss. Das folgende Rechenbeispiel zeigt dies eindrücklich. Wäre t' durch den Lorentzfaktor veränderlich, so würde folgendes rauskommen:
∆F+ma=(∆m+m)a=mvc/√(c2-v2)/t'=ma
was nicht sein kann. Der Lorentzfaktor lässt sich aufgrund der Relativität der Geschwindigkeit auch leicht ableiten. Relativ zu c ist ein Objekt mit der Geschwindigkeit v nur v√1-v2/c2 schnell. Der dimensionslose Faktor gamma^(-1) gibt also an, wie schnell v relativ zu c ist. Entgegengesetzt steigt die Trägheit des Objektes (p=mg*v/g=mv) kompensatorisch an. Dies zeigt wiederum, dass auch der Impuls mv an sich nicht veränderlich ist und dass eine dritte Größe, die veränderliche Massenträgheit, dem Impuls innewohnt.
Science Advance.
Wir benötigen Ihre Zustimmung zum Laden der Übersetzungen
Wir nutzen einen Drittanbieter-Service, um den Inhalt der Website zu übersetzen, der möglicherweise Daten über Ihre Aktivitäten sammelt. Bitte überprüfen Sie die Details in der Datenschutzerklärung und akzeptieren Sie den Dienst, um die Übersetzungen zu sehen.